1986 Total Solar Eclipse - Airborne Observations

03 October 1986
A Geometrically Remarkable Eclipse

The Annular/Total Solar Eclipse of 3 October 1986 was a remarkable event. The path, on the surface of the Earth, was a narrow, tapered, horse-shoe, and visible only from a thin strip between Iceland and Greenland. What made it remarkable was it's maximum duration - predicted by J. Meeus in 1966 in his Cannon of Solar Eclipses as "0m00s", as the mean lunar and solar topocenticlly seen semi-diameters were virtually identical. Of course, correcting for the true figure and profile of the moon, then one might expect it to be annular at sea level by some adopted values of k and definitions of totality. At maximum eclipse the solar elevation was about 6.6°. By intercepting the umbral cone from an aircraft (in our case at 40,000 feet) we were 110 km (68 miles) closer to the Moon relative to a sea level site, and thus "growing" the Moon's angular diameter with respect to the Sun by a healthy 0.8 arc seconds. That might not seem like much, but with such a marginal eclipse it made a difference. A difference significant enough to reward the nine of us who viewed this eclipse by air at such an altitude a ring of chromospheric light, and a vision of the post 3rd contact lunar shadow seen projected in its entirety like a squashed cigar on the cloud top below us. A priori, highly accurate predictions were not assured. Given the high speed of the shadow, the low altitude of the eclipse, the narrowness of the Umbra, the remoteness of the path, the uncertainties in both the lunar limb profile and refractive air-column, and the fact that GPS* wasn't yet available only the most foolish Umbraphiles would have attempted this one. Well, we did - and we were successful (though it was a planning and navigational nightmare). You'll find more which has been written about this unique eclipse, and our venture here. As it is key to an understanding of the difficulties for this eclipse, I'm also providing some information below on how we handled the refractive problem. Enquiring minds wanted to know. *GPS - Now an indespensible resource!

Every eclipse I have seen has seemed far too short. This one WAS!

19:05:16 UT

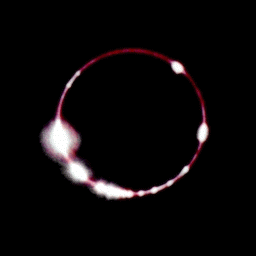
19:05:19 UT

19:05:22 UT

CLICK HERE for a montage of all 25 images at 3 frames/second with explanatory notes. Or...

CLICK HERE to view the eclipse as a QuickTime Movie. (Download a free QuickTime viewer for Mac/Windoze from Apple).

Eastern Limb at 19:05:16 UT

The "gang of 9" who were privileged to see the 3 October 1986 eclipse (at 19:05:19 U.T) stand before their Cessna Citation II chase plane, with the celebratory eclipse flag (graciously on loan from Craig Small) unfurled after a successful venture.

READ ALL ABOUT THE 1986 ECLIPSE FLIGHT

Summary Article (from "CSC Printout")

... above article, continuation

... accompanying figures [1] and [2]

THE DEVIL IS IN THE DETAILS

HOW IMPORTANT IS ATMOSPHERIC REFRACTION, ANYWAY?

For most eclipses you needn't worry. For this one it was very important.
Below are extracts from material reprinted from work I did in 1985/86, which explain this (and the above figure).

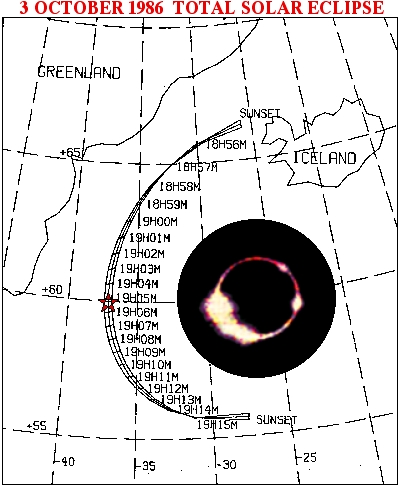
ANNULAR/TOTAL ECLIPSE OF 3 OCTOBER 1986 - CENTERLINE DATA

The tables linked here give example centerline data for the annular/total solar eclipse of 03 October 1986 for elevations (flight altitudes) of 38000, 40000, and 42000 feet above mean seal level. The data are tabulated in intervals of 30 seconds along the entire path of totality. Data for one point, on either end of the totality track, are tabulated in the annular region.

The tables contain the following information:

U.T. - Universal Time of mid-eclipse for the given latitude and longitude. The Universal Times tabulated are for an assumed Delta-T correction of 56.0 seconds.

LONGITUDE - The geographic longitude of the shadow axis for the tabulated Universal Time. If a correction to the value of Delta-T employed for the computation of these data is to be applied the new longitude can be found from: NEWLONG = LONGITUDE - 0.00417807(DELTAT - NEWDELTAT), where DELTAT and NEWDELTAT are in seconds. Tabulated longitudes were computed assuming a value of Delta-T of 56.0 seconds.

LATITUDE - The geographical latitude of the shadow axis for the tabulated Universal Time. In deriving these data the following numerical values have been used for the geodetic reference spheroid: Equatorial radius: 6378137 meters (IUGG, 1980 value), Flattening factor (f): 1/298.257 (IAU, 1976 value)

DUR - The duration of totality (or annularity) in seconds. The tabulated durations are for a smooth lunar limb and do not take into account variations which may arise from the lunar limb profile. Note, in these calculations the value of k is taken to be k=0.2725076 (where [k sin pi] is the sine of the apparent lunar semidiameter, pi is the lunar horizontal parallax.

WID The projected width of the lunar shadow, i.e. the length of the major axis of the shadow ellipse, in kilometers.

ALT The altitude of the sun above an astronomical horizon, in degrees (or 90 degrees - the zenith distance). Note that the apparent horizon, if unobstructed, will be depressed for elevations above mean sea level.

ECCNTR - The eccentricity of the projected shadow ellipse.

T - T indicates a type code, 1 for Total, 2 for annular.

These data have been corrected for the effects of atmospheric refraction. The correction for refraction is accomplished by effectively increasing the observers elevation above sea level (see the Explanatory Supplement to the A.E.N.A., page 54). In order for this to have been done, mean atmospheric temperature/pressure profiles had to be adopted. The profiles employed were derived from observations compiled by Tverskoi (1965, see appended material).

ATMOSPHERIC TEMPERATURE/PRESSURE PROFILE

The following table gives atmospheric refraction corrections to derive the apparent altitude of a celestial object above the horizon given the observer's height above mean sea level and the unrefracted altitude of the object.

The corrections given here are based on atmospheric height/temperature and height/pressure relations given by P.N. Tverskoi ("Physics of the Atmosphere", [translated from Russian] pub. Israel Program for Scientific Translations for NASA and NSF, 1965, p.57). The atmospheric data taken from this source are reproduced below in the original units (km, degrees K, and mm) and in converted units (feet, degrees C, and millibars).

Temperature and Pressure of The Atmosphere (from Tverskoi, 1965)

km °K  mm    feet   °C mbars

 0 294 757.0 0      21 1070.0

 2 278 598.0 6562    5  845.3

 4 261 466.0 13123 -12  658.7

 6 247 358.0 19685 -26  506.0

 8 233 270.0 26247 -40  381.6

10 220 201.0 32808 -53  284.1

12 217 149.0 39370 -56  210.6

16 215  79.0 52493 -58  111.7

20 216  41.9 65617 -57   59.2

The refraction correction table gives the correction, in minutes of arc, to be applied to the unrefracted altitude of the object, in degrees, given the observers height above MSL. The table is tabulated for observer heights in the range of 0 to 50000 feet in 1000 foot increments, and object altitudes of 0 to 10 degrees in increments of 0.5 degrees. Temperatures and pressures for the refraction model at each observer height were obtained by a cubical spline fit to the above table. The direction of the correction is toward the zenith.

**Tables of Atmospheric Refraction Corrections in arc minutes Toward Zenith - 0-50,000 feet, 0°-10°.**
Atmospheric Refraction Correction Table Observers Height Above MSL vs. Unrefracted Altitude Above Horizon Corrections in Arc-Minutes Toward the Zenith HEIGH TEMP PRESS ------ OBJECT ALTITUDE ABOVE HORIZON IN DEGREES ------- Feet DegC mbars 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 ----- ---- ------ ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- 0 21.0 1070.0 34.8 29.0 24.6 21.2 18.5 16.3 14.6 13.1 11.9 10.9 10.0 1000 18.6 1034.5 33.9 28.3 24.0 20.6 18.0 15.9 14.2 12.8 11.6 10.6 9.7 2000 16.3 999.2 33.0 27.5 23.3 20.1 17.5 15.5 13.8 12.4 11.3 10.3 9.5 3000 13.9 964.3 32.1 26.8 22.7 19.6 17.1 15.1 13.4 12.1 11.0 10.0 9.2 4000 11.4 929.8 31.3 26.1 22.1 19.0 16.6 14.7 13.1 11.8 10.7 9.8 9.0 5000 9.0 896.1 30.4 25.3 21.5 18.5 16.1 14.2 12.7 11.4 10.4 9.5 8.7 6000 6.4 863.3 29.5 24.6 20.9 18.0 15.7 13.9 12.4 11.1 10.1 9.2 8.5 7000 3.9 831.5 28.7 23.9 20.3 17.5 15.2 13.5 12.0 10.8 9.8 9.0 8.2 8000 1.2 800.8 27.9 23.3 19.7 17.0 14.8 13.1 11.7 10.5 9.5 8.7 8.0 9000 -1.4 771.1 27.2 22.6 19.2 16.5 14.4 12.7 11.4 10.2 9.3 8.5 7.8 10000 -4.1 742.5 26.4 22.0 18.7 16.1 14.0 12.4 11.0 9.9 9.0 8.2 7.6 11000 -6.7 714.8 25.7 21.4 18.1 15.6 13.6 12.0 10.7 9.7 8.8 8.0 7.4 12000 -9.2 687.9 24.9 20.8 17.6 15.2 13.2 11.7 10.4 9.4 8.5 7.8 7.2 13000 -11.7 661.8 24.2 20.2 17.1 14.7 12.9 11.4 10.1 9.1 8.3 7.6 7.0 14000 -14.0 636.5 23.5 19.6 16.6 14.3 12.5 11.0 9.8 8.9 8.0 7.3 6.7 15000 -16.3 611.9 22.8 19.0 16.1 13.9 12.1 10.7 9.5 8.6 7.8 7.1 6.5 16000 -18.4 588.0 22.1 18.4 15.6 13.4 11.7 10.4 9.2 8.3 7.5 6.9 6.3 17000 -20.5 564.8 21.4 17.8 15.1 13.0 11.4 10.0 8.9 8.1 7.3 6.7 6.1 18000 -22.6 542.3 20.7 17.3 14.6 12.6 11.0 9.7 8.7 7.8 7.1 6.5 5.9 19000 -24.6 520.6 20.0 16.7 14.2 12.2 10.6 9.4 8.4 7.5 6.8 6.3 5.8 20000 -26.6 499.5 19.4 16.2 13.7 11.8 10.3 9.1 8.1 7.3 6.6 6.1 5.6 21000 -28.7 479.0 18.8 15.6 13.2 11.4 10.0 8.8 7.8 7.1 6.4 5.9 5.4 22000 -30.8 459.2 18.1 15.1 12.8 11.0 9.6 8.5 7.6 6.8 6.2 5.7 5.2 23000 -32.9 440.1 17.5 14.6 12.4 10.7 9.3 8.2 7.3 6.6 6.0 5.5 5.0 24000 -35.0 421.5 16.9 14.1 12.0 10.3 9.0 7.9 7.1 6.4 5.8 5.3 4.9 25000 -37.2 403.4 16.4 13.6 11.6 10.0 8.7 7.7 6.8 6.2 5.6 5.1 4.7 26000 -39.4 385.9 15.8 13.2 11.2 9.6 8.4 7.4 6.6 6.0 5.4 4.9 4.5 27000 -41.7 368.9 15.3 12.7 10.8 9.3 8.1 7.2 6.4 5.7 5.2 4.8 4.4 28000 -44.0 352.4 14.7 12.3 10.4 9.0 7.8 6.9 6.2 5.5 5.0 4.6 4.2 29000 -46.3 336.6 14.2 11.8 10.0 8.6 7.5 6.7 5.9 5.3 4.9 4.4 4.1 30000 -48.4 321.5 13.7 11.4 9.7 8.3 7.3 6.4 5.7 5.2 4.7 4.3 3.9 31000 -50.3 307.3 13.2 11.0 9.3 8.0 7.0 6.2 5.5 5.0 4.5 4.1 3.8 32000 -51.9 294.1 12.7 10.6 9.0 7.7 6.8 6.0 5.3 4.8 4.3 4.0 3.7 33000 -53.2 281.9 12.3 10.2 8.7 7.5 6.5 5.7 5.1 4.6 4.2 3.8 3.5 34000 -54.2 270.7 11.8 9.9 8.4 7.2 6.3 5.5 4.9 4.5 4.0 3.7 3.4 35000 -54.8 260.1 11.4 9.5 8.1 6.9 6.1 5.3 4.8 4.3 3.9 3.6 3.3 36000 -55.3 249.8 11.0 9.1 7.8 6.7 5.8 5.1 4.6 4.1 3.7 3.4 3.1 37000 -55.5 239.2 10.5 8.8 7.4 6.4 5.6 4.9 4.4 4.0 3.6 3.3 3.0 38000 -55.7 227.9 10.0 8.4 7.1 6.1 5.3 4.7 4.2 3.8 3.4 3.1 2.9 39000 -55.9 215.5 9.5 7.9 8.7 5.8 5.0 4.5 4.0 3.6 3.2 3.0 2.7 40000 -56.1 206.2 9.1 7.6 6.4 5.5 4.8 4.3 3.8 3.4 3.1 2.8 2.6 41000 -56.2 199.0 8.8 7.3 6.2 5.3 4.7 4.1 3.7 3.3 3.0 2.7 2.5 42000 -56.4 191.4 8.5 7.0 6.0 5.1 4.5 4.0 3.5 3.2 2.9 2.6 2.4 43000 -56.6 183.7 8.1 6.8 5.7 4.9 4.3 3.8 3.4 3.1 2.8 2.5 2.3 44000 -56.7 175.7 7.8 6.5 5.5 4.7 4.1 3.6 3.3 2.9 2.7 2.4 2.2 45000 -56.9 167.7 7.4 6.2 5.2 4.5 3.9 3.5 3.1 2.8 2.5 2.3 2.1 46000 -57.1 159.6 7.1 5.9 5.0 4.3 3.8 3.3 3.0 2.7 2.4 2.2 2.0 47000 -57.3 151.6 6.7 5.6 4.7 4.1 3.6 3.2 2.8 2.5 2.3 2.1 1.9 48000 -57.5 143.7 6.4 5.3 4.5 3.9 3.4 3.0 2.7 2.4 2.2 2.0 1.8 49000 -57.6 136.0 6.0 5.0 4.3 3.7 3.2 2.8 2.5 2.3 2.1 1.9 1.7 50000 -57.8 128.6 5.7 4.8 4.0 3.5 3.0 2.7 2.4 2.2 2.0 1.8 1.6
HEIGH TEMP PRESS --- OBJECT ALTITUDE ABOVE HORIZON IN DEGREES ----- Feet DegC mbars 5.5 6.0 6.5 7.0 7.5 8.0 8.5 9.0 9.5 10.0 ----- ---- ------ ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- 0 21.0 1070.0 9.2 8.6 8.0 7.5 7.0 6.6 6.3 5.9 5.7 5.4 1000 18.6 1034.5 9.0 8.4 7.8 7.3 6.9 6.5 6.1 5.8 5.5 5.2 2000 16.3 999.2 8.8 8.1 7.6 7.1 6.7 6.3 6.0 5.6 5.4 5.1 3000 13.9 964.3 8.5 7.9 7.4 6.9 6.5 6.1 5.8 5.5 5.2 5.0 4000 11.4 929.8 8.3 7.7 7.2 6.7 6.3 6.0 5.6 5.3 5.1 4.8 5000 9.0 896.1 8.1 7.5 7.0 6.5 6.1 5.8 5.5 5.2 4.9 4.7 6000 6.4 863.3 7.8 7.3 6.8 6.4 6.0 5.6 5.3 5.0 4.8 4.6 7000 3.9 831.5 7.6 7.1 6.6 6.2 5.8 5.5 5.2 4.9 4.7 4.4 8000 1.2 800.8 7.4 6.9 6.4 6.0 5.6 5.3 5.0 4.8 4.5 4.3 9000 -1.4 771.1 7.2 6.7 6.2 5.8 5.5 5.2 4.9 4.6 4.4 4.2 10000 -4.1 742.5 7.0 6.5 6.1 5.7 5.3 5.0 4.8 4.5 4.3 4.1 11000 -6.7 714.8 6.8 6.3 5.9 5.5 5.2 4.9 4.6 4.4 4.2 4.0 12000 -9.2 687.9 6.6 6.1 5.7 5.4 5.0 4.8 4.5 4.3 4.0 3.9 13000 -11.7 661.8 6.4 6.0 5.6 5.2 4.9 4.6 4.4 4.1 3.9 3.7 14000 -14.0 636.5 6.2 5.8 5.4 5.1 4.8 4.5 4.2 4.0 3.8 3.6 15000 -16.3 611.9 6.0 5.6 5.2 4.9 4.6 4.3 4.1 3.9 3.7 3.5 16000 -18.4 588.0 5.9 5.4 5.1 4.8 4.5 4.2 4.0 3.8 3.6 3.4 17000 -20.5 564.8 5.7 5.3 4.9 4.6 4.3 4.1 3.9 3.7 3.5 3.3 18000 -22.6 542.3 5.5 5.1 4.8 4.5 4.2 3.9 3.7 3.5 3.4 3.2 19000 -24.6 520.6 5.3 4.9 4.6 4.3 4.1 3.8 3.6 3.4 3.3 3.1 20000 -26.6 499.5 5.1 4.8 4.5 4.2 3.9 3.7 3.5 3.3 3.1 3.0 21000 -28.7 479.0 5.0 4.6 4.3 4.0 3.8 3.6 3.4 3.2 3.0 2.9 22000 -30.8 459.2 4.8 4.5 4.2 3.9 3.7 3.5 3.3 3.1 2.9 2.8 23000 -32.9 440.1 4.6 4.3 4.0 3.8 3.5 3.3 3.2 3.0 2.8 2.7 24000 -35.0 421.5 4.5 4.2 3.9 3.6 3.4 3.2 3.1 2.9 2.7 2.6 25000 -37.2 403.4 4.3 4.0 3.8 3.5 3.3 3.1 2.9 2.8 2.7 2.5 26000 -39.4 385.9 4.2 3.9 3.6 3.4 3.2 3.0 2.8 2.7 2.6 2.4 27000 -41.7 368.9 4.0 3.8 3.5 3.3 3.1 2.9 2.7 2.6 2.5 2.4 28000 -44.0 352.4 3.9 3.6 3.4 3.2 3.0 2.8 2.7 2.5 2.4 2.3 29000 -46.3 336.6 3.8 3.5 3.3 3.1 2.9 2.7 2.6 2.4 2.3 2.2 30000 -48.4 321.5 3.6 3.4 3.1 2.9 2.8 2.6 2.5 2.3 2.2 2.1 31000 -50.3 307.3 3.5 3.3 3.0 2.8 2.7 2.5 2.4 2.3 2.1 2.0 32000 -51.9 294.1 3.4 3.1 2.9 2.7 2.6 2.4 2.3 2.2 2.1 2.0 33000 -53.2 281.9 3.3 3.0 2.8 2.6 2.5 2.3 2.2 2.1 2.0 1.9 34000 -54.2 270.7 3.1 2.9 2.7 2.5 2.4 2.3 2.1 2.0 1.9 1.8 35000 -54.8 260.1 3.0 2.8 2.6 2.5 2.3 2.2 2.1 1.9 1.9 1.8 36000 -55.3 249.8 2.9 2.7 2.5 2.4 2.2 2.1 2.0 1.9 1.8 1.7 37000 -55.5 239.2 2.8 2.6 2.4 2.3 2.1 2.0 1.9 1.8 1.7 1.6 38000 -55.7 227.9 2.7 2.5 2.3 2.2 2.0 1.9 1.8 1.7 1.6 1.6 39000 -55.9 215.5 2.5 2.3 2.2 2.0 1.9 1.8 1.7 1.6 1.5 1.5 40000 -56.1 206.2 2.4 2.2 2.1 2.0 1.8 1.7 1.6 1.6 1.5 1.4 41000 -56.2 199.0 2.3 2.2 2.0 1.9 1.8 1.7 1.6 1.5 1.4 1.4 42000 -56.4 191.4 2.2 2.1 1.9 1.8 1.7 1.6 1.5 1.4 1.4 1.3 43000 -56.6 183.7 2.2 2.0 1.9 1.7 1.6 1.5 1.5 1.4 1.3 1.3 44000 -56.7 175.7 2.1 1.9 1.8 1.7 1.6 1.5 1.4 1.3 1.3 1.2 45000 -56.9 167.7 2.0 1.8 1.7 1.6 1.5 1.4 1.3 1.3 1.2 1.1 46000 -57.1 159.6 1.9 1.7 1.6 1.5 1.4 1.3 1.3 1.2 1.1 1.1 47000 -57.3 151.6 1.8 1.7 1.5 1.4 1.4 1.3 1.2 1.1 1.1 1.0 48000 -57.5 143.7 1.7 1.6 1.5 1.4 1.3 1.2 1.1 1.1 1.0 1.0 49000 -57.6 136.0 1.6 1.5 1.4 1.3 1.2 1.2 1.1 1.0 1.0 0.9 50000 -57.8 128.6 1.5 1.4 1.3 1.2 1.2 1.1 1.0 1.0 0.9 0.9

Tables of Atmospheric Refraction Corrections in arc minutes Toward Zenith - 0-50,000 feet, 0°-10°.

Atmospheric Refraction Correction Table
Observers Height Above MSL vs. Unrefracted Altitude Above Horizon
Corrections in Arc-Minutes Toward the Zenith

HEIGH   TEMP PRESS ------ OBJECT ALTITUDE ABOVE HORIZON IN DEGREES -------
Feet    DegC mbars   0.0  0.5  1.0  1.5  2.0  2.5  3.0  3.5  4.0  4.5  5.0
-----   ---- ------ ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
0       21.0 1070.0 34.8 29.0 24.6 21.2 18.5 16.3 14.6 13.1 11.9 10.9 10.0
1000    18.6 1034.5 33.9 28.3 24.0 20.6 18.0 15.9 14.2 12.8 11.6 10.6  9.7
2000    16.3  999.2 33.0 27.5 23.3 20.1 17.5 15.5 13.8 12.4 11.3 10.3  9.5
3000    13.9  964.3 32.1 26.8 22.7 19.6 17.1 15.1 13.4 12.1 11.0 10.0  9.2
4000    11.4  929.8 31.3 26.1 22.1 19.0 16.6 14.7 13.1 11.8 10.7  9.8  9.0
5000     9.0  896.1 30.4 25.3 21.5 18.5 16.1 14.2 12.7 11.4 10.4  9.5  8.7
6000     6.4  863.3 29.5 24.6 20.9 18.0 15.7 13.9 12.4 11.1 10.1  9.2  8.5
7000     3.9  831.5 28.7 23.9 20.3 17.5 15.2 13.5 12.0 10.8  9.8  9.0  8.2
8000     1.2  800.8 27.9 23.3 19.7 17.0 14.8 13.1 11.7 10.5  9.5  8.7  8.0
9000    -1.4  771.1 27.2 22.6 19.2 16.5 14.4 12.7 11.4 10.2  9.3  8.5  7.8
10000   -4.1  742.5 26.4 22.0 18.7 16.1 14.0 12.4 11.0  9.9  9.0  8.2  7.6
11000   -6.7  714.8 25.7 21.4 18.1 15.6 13.6 12.0 10.7  9.7  8.8  8.0  7.4
12000   -9.2  687.9 24.9 20.8 17.6 15.2 13.2 11.7 10.4  9.4  8.5  7.8  7.2
13000  -11.7  661.8 24.2 20.2 17.1 14.7 12.9 11.4 10.1  9.1  8.3  7.6  7.0
14000  -14.0  636.5 23.5 19.6 16.6 14.3 12.5 11.0  9.8  8.9  8.0  7.3  6.7
15000  -16.3  611.9 22.8 19.0 16.1 13.9 12.1 10.7  9.5  8.6  7.8  7.1  6.5
16000  -18.4  588.0 22.1 18.4 15.6 13.4 11.7 10.4  9.2  8.3  7.5  6.9  6.3
17000  -20.5  564.8 21.4 17.8 15.1 13.0 11.4 10.0  8.9  8.1  7.3  6.7  6.1
18000  -22.6  542.3 20.7 17.3 14.6 12.6 11.0  9.7  8.7  7.8  7.1  6.5  5.9
19000  -24.6  520.6 20.0 16.7 14.2 12.2 10.6  9.4  8.4  7.5  6.8  6.3  5.8
20000  -26.6  499.5 19.4 16.2 13.7 11.8 10.3  9.1  8.1  7.3  6.6  6.1  5.6
21000  -28.7  479.0 18.8 15.6 13.2 11.4 10.0  8.8  7.8  7.1  6.4  5.9  5.4
22000  -30.8  459.2 18.1 15.1 12.8 11.0  9.6  8.5  7.6  6.8  6.2  5.7  5.2
23000  -32.9  440.1 17.5 14.6 12.4 10.7  9.3  8.2  7.3  6.6  6.0  5.5  5.0
24000  -35.0  421.5 16.9 14.1 12.0 10.3  9.0  7.9  7.1  6.4  5.8  5.3  4.9
25000  -37.2  403.4 16.4 13.6 11.6 10.0  8.7  7.7  6.8  6.2  5.6  5.1  4.7
26000  -39.4  385.9 15.8 13.2 11.2  9.6  8.4  7.4  6.6  6.0  5.4  4.9  4.5
27000  -41.7  368.9 15.3 12.7 10.8  9.3  8.1  7.2  6.4  5.7  5.2  4.8  4.4
28000  -44.0  352.4 14.7 12.3 10.4  9.0  7.8  6.9  6.2  5.5  5.0  4.6  4.2
29000  -46.3  336.6 14.2 11.8 10.0  8.6  7.5  6.7  5.9  5.3  4.9  4.4  4.1
30000  -48.4  321.5 13.7 11.4  9.7  8.3  7.3  6.4  5.7  5.2  4.7  4.3  3.9
31000  -50.3  307.3 13.2 11.0  9.3  8.0  7.0  6.2  5.5  5.0  4.5  4.1  3.8
32000  -51.9  294.1 12.7 10.6  9.0  7.7  6.8  6.0  5.3  4.8  4.3  4.0  3.7
33000  -53.2  281.9 12.3 10.2  8.7  7.5  6.5  5.7  5.1  4.6  4.2  3.8  3.5
34000  -54.2  270.7 11.8  9.9  8.4  7.2  6.3  5.5  4.9  4.5  4.0  3.7  3.4
35000  -54.8  260.1 11.4  9.5  8.1  6.9  6.1  5.3  4.8  4.3  3.9  3.6  3.3
36000  -55.3  249.8 11.0  9.1  7.8  6.7  5.8  5.1  4.6  4.1  3.7  3.4  3.1
37000  -55.5  239.2 10.5  8.8  7.4  6.4  5.6  4.9  4.4  4.0  3.6  3.3  3.0
38000  -55.7  227.9 10.0  8.4  7.1  6.1  5.3  4.7  4.2  3.8  3.4  3.1  2.9
39000  -55.9  215.5  9.5  7.9  8.7  5.8  5.0  4.5  4.0  3.6  3.2  3.0  2.7
40000  -56.1  206.2  9.1  7.6  6.4  5.5  4.8  4.3  3.8  3.4  3.1  2.8  2.6
41000  -56.2  199.0  8.8  7.3  6.2  5.3  4.7  4.1  3.7  3.3  3.0  2.7  2.5
42000  -56.4  191.4  8.5  7.0  6.0  5.1  4.5  4.0  3.5  3.2  2.9  2.6  2.4
43000  -56.6  183.7  8.1  6.8  5.7  4.9  4.3  3.8  3.4  3.1  2.8  2.5  2.3
44000  -56.7  175.7  7.8  6.5  5.5  4.7  4.1  3.6  3.3  2.9  2.7  2.4  2.2
45000  -56.9  167.7  7.4  6.2  5.2  4.5  3.9  3.5  3.1  2.8  2.5  2.3  2.1
46000  -57.1  159.6  7.1  5.9  5.0  4.3  3.8  3.3  3.0  2.7  2.4  2.2  2.0
47000  -57.3  151.6  6.7  5.6  4.7  4.1  3.6  3.2  2.8  2.5  2.3  2.1  1.9
48000  -57.5  143.7  6.4  5.3  4.5  3.9  3.4  3.0  2.7  2.4  2.2  2.0  1.8
49000  -57.6  136.0  6.0  5.0  4.3  3.7  3.2  2.8  2.5  2.3  2.1  1.9  1.7
50000  -57.8  128.6  5.7  4.8  4.0  3.5  3.0  2.7  2.4  2.2  2.0  1.8  1.6

HEIGH   TEMP PRESS --- OBJECT ALTITUDE ABOVE HORIZON IN DEGREES -----
Feet    DegC mbars   5.5  6.0  6.5  7.0  7.5  8.0  8.5  9.0  9.5 10.0
-----   ---- ------ ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
    0   21.0 1070.0  9.2  8.6  8.0  7.5  7.0  6.6  6.3  5.9  5.7  5.4
 1000   18.6 1034.5  9.0  8.4  7.8  7.3  6.9  6.5  6.1  5.8  5.5  5.2
 2000   16.3  999.2  8.8  8.1  7.6  7.1  6.7  6.3  6.0  5.6  5.4  5.1
 3000   13.9  964.3  8.5  7.9  7.4  6.9  6.5  6.1  5.8  5.5  5.2  5.0
 4000   11.4  929.8  8.3  7.7  7.2  6.7  6.3  6.0  5.6  5.3  5.1  4.8
 5000    9.0  896.1  8.1  7.5  7.0  6.5  6.1  5.8  5.5  5.2  4.9  4.7
 6000    6.4  863.3  7.8  7.3  6.8  6.4  6.0  5.6  5.3  5.0  4.8  4.6
 7000    3.9  831.5  7.6  7.1  6.6  6.2  5.8  5.5  5.2  4.9  4.7  4.4
 8000    1.2  800.8  7.4  6.9  6.4  6.0  5.6  5.3  5.0  4.8  4.5  4.3
 9000   -1.4  771.1  7.2  6.7  6.2  5.8  5.5  5.2  4.9  4.6  4.4  4.2
10000   -4.1  742.5  7.0  6.5  6.1  5.7  5.3  5.0  4.8  4.5  4.3  4.1
11000   -6.7  714.8  6.8  6.3  5.9  5.5  5.2  4.9  4.6  4.4  4.2  4.0
12000   -9.2  687.9  6.6  6.1  5.7  5.4  5.0  4.8  4.5  4.3  4.0  3.9
13000  -11.7  661.8  6.4  6.0  5.6  5.2  4.9  4.6  4.4  4.1  3.9  3.7
14000  -14.0  636.5  6.2  5.8  5.4  5.1  4.8  4.5  4.2  4.0  3.8  3.6
15000  -16.3  611.9  6.0  5.6  5.2  4.9  4.6  4.3  4.1  3.9  3.7  3.5
16000  -18.4  588.0  5.9  5.4  5.1  4.8  4.5  4.2  4.0  3.8  3.6  3.4
17000  -20.5  564.8  5.7  5.3  4.9  4.6  4.3  4.1  3.9  3.7  3.5  3.3
18000  -22.6  542.3  5.5  5.1  4.8  4.5  4.2  3.9  3.7  3.5  3.4  3.2
19000  -24.6  520.6  5.3  4.9  4.6  4.3  4.1  3.8  3.6  3.4  3.3  3.1
20000  -26.6  499.5  5.1  4.8  4.5  4.2  3.9  3.7  3.5  3.3  3.1  3.0
21000  -28.7  479.0  5.0  4.6  4.3  4.0  3.8  3.6  3.4  3.2  3.0  2.9
22000  -30.8  459.2  4.8  4.5  4.2  3.9  3.7  3.5  3.3  3.1  2.9  2.8
23000  -32.9  440.1  4.6  4.3  4.0  3.8  3.5  3.3  3.2  3.0  2.8  2.7
24000  -35.0  421.5  4.5  4.2  3.9  3.6  3.4  3.2  3.1  2.9  2.7  2.6
25000  -37.2  403.4  4.3  4.0  3.8  3.5  3.3  3.1  2.9  2.8  2.7  2.5
26000  -39.4  385.9  4.2  3.9  3.6  3.4  3.2  3.0  2.8  2.7  2.6  2.4
27000  -41.7  368.9  4.0  3.8  3.5  3.3  3.1  2.9  2.7  2.6  2.5  2.4
28000  -44.0  352.4  3.9  3.6  3.4  3.2  3.0  2.8  2.7  2.5  2.4  2.3
29000  -46.3  336.6  3.8  3.5  3.3  3.1  2.9  2.7  2.6  2.4  2.3  2.2
30000  -48.4  321.5  3.6  3.4  3.1  2.9  2.8  2.6  2.5  2.3  2.2  2.1
31000  -50.3  307.3  3.5  3.3  3.0  2.8  2.7  2.5  2.4  2.3  2.1  2.0
32000  -51.9  294.1  3.4  3.1  2.9  2.7  2.6  2.4  2.3  2.2  2.1  2.0
33000  -53.2  281.9  3.3  3.0  2.8  2.6  2.5  2.3  2.2  2.1  2.0  1.9
34000  -54.2  270.7  3.1  2.9  2.7  2.5  2.4  2.3  2.1  2.0  1.9  1.8
35000  -54.8  260.1  3.0  2.8  2.6  2.5  2.3  2.2  2.1  1.9  1.9  1.8
36000  -55.3  249.8  2.9  2.7  2.5  2.4  2.2  2.1  2.0  1.9  1.8  1.7
37000  -55.5  239.2  2.8  2.6  2.4  2.3  2.1  2.0  1.9  1.8  1.7  1.6
38000  -55.7  227.9  2.7  2.5  2.3  2.2  2.0  1.9  1.8  1.7  1.6  1.6
39000  -55.9  215.5  2.5  2.3  2.2  2.0  1.9  1.8  1.7  1.6  1.5  1.5
40000  -56.1  206.2  2.4  2.2  2.1  2.0  1.8  1.7  1.6  1.6  1.5  1.4
41000  -56.2  199.0  2.3  2.2  2.0  1.9  1.8  1.7  1.6  1.5  1.4  1.4
42000  -56.4  191.4  2.2  2.1  1.9  1.8  1.7  1.6  1.5  1.4  1.4  1.3
43000  -56.6  183.7  2.2  2.0  1.9  1.7  1.6  1.5  1.5  1.4  1.3  1.3
44000  -56.7  175.7  2.1  1.9  1.8  1.7  1.6  1.5  1.4  1.3  1.3  1.2
45000  -56.9  167.7  2.0  1.8  1.7  1.6  1.5  1.4  1.3  1.3  1.2  1.1
46000  -57.1  159.6  1.9  1.7  1.6  1.5  1.4  1.3  1.3  1.2  1.1  1.1
47000  -57.3  151.6  1.8  1.7  1.5  1.4  1.4  1.3  1.2  1.1  1.1  1.0
48000  -57.5  143.7  1.7  1.6  1.5  1.4  1.3  1.2  1.1  1.1  1.0  1.0
49000  -57.6  136.0  1.6  1.5  1.4  1.3  1.2  1.2  1.1  1.0  1.0  0.9
50000  -57.8  128.6  1.5  1.4  1.3  1.2  1.2  1.1  1.0  1.0  0.9  0.9

The temperatures and pressures assumed for the tracks, at the tabulated elevations, were obtained from a cubicle spline fit to these profiles.

The degree of refraction, as a function of zenith distance, was computed as the ratio of two truncated power series parameterized by the pressure and temperature at a given elevation. (See the 1987 Astronomical Almanac, page B62). This was compared to the degree of refraction at sea level, to derive an effective refractive index for the airpath. From this, the observers effective elevation was derived (see Chauvenet, Vol. 1, p. 516).

CENTERLINE TRACKS

The centerline tracks for the 03 October 1986 eclipse, for the tabulated elevations above mean sea level (38000, 40000 and 42000 feet), are depicted on the accompanying orthographic projection map. The leftmost of the three roughly parallel curves is the centerline at 42000 feet, the center curve corresponds to an elevation of 40000 feet and the rightmost 38000 feet.

The centerlines run, in Universal Time, from 18h55m to 19hl6m. This completely covers the path of totality, but includes only a short segment of the path of annularity at the ends of the curves. Time tics for each minute of Universal Time are shown on the map.

The coordinates of the points plotted on the eclipse map are taken from the tabulated centerline data.

Correcting for both the aircraft altitude, and atmospheric refraction at 3 different altitudes, the centerline tracks for 18:55UT- 19:16-UT were as follows:

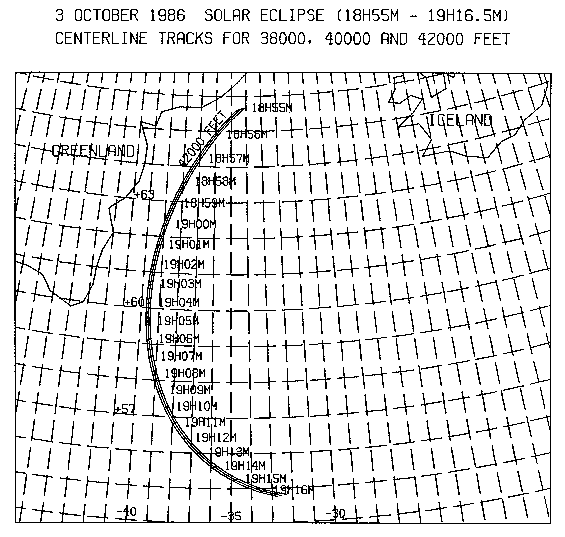
Or, in a bit more detail, with a change in altitude of 12,000 feet the path shifts, even at maximum eclipse, by more than its width.

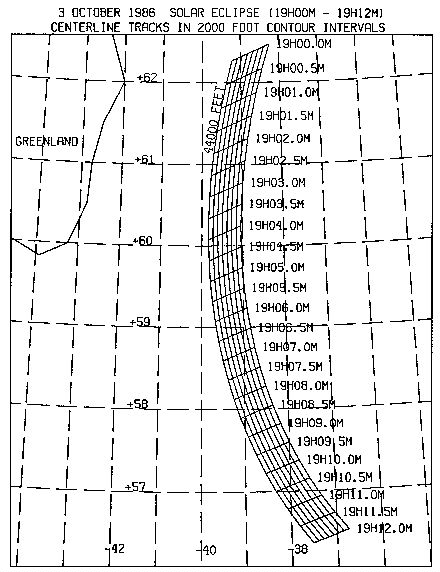
For this eclipse it was CRITICAL to be centrally located within the limb-corrected shadow.

LIMB PROFILE

Alan Fiala (USNO) kindly provided us with a prediction of the limb profile for 19:06 and 19:07 U.T. from sea level. As can be seen, the topocentric prediction indicated incomplete photospheric extinction.
Compare the morphology of the limb features in this prediction with the photograph above taken at 19:05:19 UT. Though our mid-eclipse intercept was 40 seconds earlier than the time of first limb prediction, the topocentric librational differences are insignificant. Looks like within the systematic uncertainties, we nailed it.

And, What Did The Icelandic Newspaper, the MORGUNBLADID, have to say about this?

Well, if you can read THIS let me know!

Glenn Schneider