Glenn Schneider
Steward Observatory
933 N. Cherry Avenue
University of Arizona
Tucson, Arizona 85750
gschneider@as.arizona.edu
or gschneider@mac.com
INTRODUCTION
The total solar eclipse of 23 November 2003 poses some
very challenging logistical problems in organizing an observing expedition.
The weather on the Antarctic coast at that time of year is often cloudy,
accompanied by high winds, and mobility in the path of totality on the
continent is severely limited. The inland plateau is generally
inaccessible along the path. Some have opted to secure the use of
an ice breaker for transport and/or shipboard observation - but the costs
are high, the duration of travel is long, and while some further
cloud-escaping mobility is offered, success is still questionable.
For some, such as myself, it appears that the most viable option for observing
the Total Solar Eclipse of 23 November 2003 is from
the air. The total phase of the eclipse becomes visible at
sunrise at a latitude of 52.5 degrees S, southwest of Australia, then moves
southward toward the Antarctic, and traverses the continent from approximately
longitudes 80E to 15E. While at least one Antarctic over flights
is in consideration, it is not necessary (though to some it may be very
understandably desirable), as an airborne observation in the path of totality
over the Ocean well north of 60S is a viable alternative. Thus, there
are two philosophies, neither wrong or right, just different, on how to
approach this:
1) CRYODON TRAVEL
"Tourist" flights over the Antarctic are implemented on a regular basis by Cryodon Travel, an Australian based company. Phil Asker, managing director, had indicated in earlier correspondences that Cryodon will likely plan a variant of their "regular" Antarctic overflight to include a fly through the path of totality during the eclipse. Though, details of that have not yet been made available. Cryodon uses a 747-438 aircraft for their air tours. This is a wonderful aircraft, but may be more than is needed for a planed, dedicated, eclipse flight where the eclipse observation is the primary objective. Cryodon normally does their Antarctic tours with a full (or nearly so) cabin. For that, they have implemented a "seat rotation" plan to allow site-seers shared viewing time when flying over the Antarctic, priced by class and land-visability below the aircraft wing. This is likely a very good, and well used method for site-seeing flights, but with less than 2 minutes of totality a dedicated window is needed for an eclipse observer. An earlier concept discussed was to one of their "regular" Antarctic overflights, but, on the way down "add in" the eclipse, with only eclipse viewers only on the sun-side windows. Eclipse viewers would either pay a premium for this and take a non-rotating "middle" seat after the eclipse while the Antarctic tourists rotate around them - or some variant thereof. The seating configuration on the Cryodon web site seems to match the 416 total seat layout as one of the possible ways to configure a 747-400. I do not know with certainty if that is how the aircraft Cryodon uses is arranged (perhaps they can advise?). Boeing does not list a 747-438 as one of the 747 family, but as this is certainly a derivative of the 747-400/747ER aircraft family. Those planes have, on the sun-side of the aircraft: 54 windows in the economy class section, 14 in business, 14 in first, 21 upper deck, and 5 in the doors. If the seat layout is different then the windows may not map to sections of the aircraft - and I have no idea as to how the cadence of the seats matched (or does not match) the windows (perhaps Cryodon can advise here as well?).
In a preliminary public
release about Cryodon's plans, they say they intend to observe
from near Myrny and then go on to do a siteseeing flight. The costing
is not clear as the release says prices start at $700 US with "premiums
applying to those who wish to have window seats during the actual time
of the eclipse". The base price is certainly a bargain (if it is
correct?), with the non eclipse-watchers, obviously, subsidizing the very
high window-to-seat ratio for the eclipse. But what is the premium to be?
The concept is intriguing, and certainly bears very serious consideration.
Unless of course you have...
2) A SOMEWHAT DIFFERENT PERSPECTIVE
The economic viability of chartering a commercially suitable aircraft for a dedicated and planned airborne eclipse observation, unconcerned with concomitant site-seeing, is predicated on assessing the cost per window on the "sun side" of the aircraft, not the cost per seat. Normal aircraft seating configurations pay no head to the cadence of windows and seats. Hence, from some "window seats" windows can be ill-placed or even inaccessible, while others may have access to more than one window. For an "eclipse flight", a multi-passenger jet becomes a viable, indeed desirable, observing platform by removing the row of seats immediately seats immediately adjacent to the wall of Sun side windows. For nearly all aircraft the seats are latched to the floor decking by "rails" and are very easily removed. Once that is done, sun-side of the aircraft floor becomes an observing platform, where observers can position themselves, and their equipment, in a comfortable, and equitable manner. Indeed, with prior co-operation and consent the air charter company, it is quite easy to fashion a camera/equipment mount to latch into the seat rails after the seats are removed. For take-off and landing the reduced-from-normal number of passengers are seated in the middle or anti-sun side seats.
From here on when I refer to the "number of windows" that should implicitly be taken to mean the number of usable windows on the sun-side of the aircraft. In a baseline per-person cost assessment, a window is equated to a person (not as in the case of a "normal" charter where a seat [assuming the aircraft is filled] is equated to a person). Here, we must evaluate the per-window cost. It is possible, of course, for two people to have planned and agreed in advance to share a window, and hence share the cost of a window. This is a personal and individual decision, as most (if not all) eclipse observers would opt for an individual window if the costs were not prohibitive. The actual cost of charting an aircraft depends upon:
a) The distance flown (or time-in-flight)
b) The amount of fuel consumed (obviously,
dependent upon [a]).
c) The the of aircraft used (selected based
upon [a], [d], and availability/utility).
d) The "overhead" flight and ground crew
time and company/equipment costs not predicated on a variable time/distance
basis.
A) Total Flight Distance
Because of the geometry of this eclipse, to reach any point along centerline of the path of totality, the total flight distance is minimized by launching a flight from SW, Australia. Here, I consider Perth, as that closest, nearest, major airport to any point in the path of totality. One can see this simply looking at a hemispheric map of the eclipse such as this one by Espenak at sea level. If an suitable aircraft cannot be secured from Perth, somewhat more distant locations (such as Melbourne) can easily be evaluated. The location of the path of totality (and the circumstances of the eclipse along it) change with an observer's altitude above mean sea level. This is shown on a chart of the Path of Totality at 0, 20,000, and 40,000 feet. For comparative purposes, I have produced this chart at the same scale and orientation as a sea level map of the path over the Antarctic by Espenak (which covers a larger area including additional regions where the eclipse will be seen as a large magnitude partial}. For discussion and illustration, I have taken 12km (appx. 40,000 ft) as canonical cruising altitude for any of the high-altitude long-range jet aircraft which might be considered (though actual flight levels may, of course, vary). Centerline circumstances at 12km altitude for locations corresponding to the time from shortly after sunrise (at 22h 22m 00s UT; at the closer-to-Australia end of the track) through 22h 25m 30s UT are tabulated below along with the corresponding topocentric distance of that point to the Perth airport. For planning and discussion purposes, I have done this only at a time-step of 15 seconds, but this is more than sufficient to identify the near-point to Perth and proceed with initial plans.
ECLIPSE-23NOV2003_240.DATA Topographic Elevation = 12000 meters
above MSL
HH MM SS.f LONGITUDE_______________ LATITUDE_____________ DUR
s W km ALTd AZIMd ECCEN PERTH km
22 22 00.0 +84.4454 (+084 26 43.4) -53.0058 (-53 00 21.0) 098.5
510.2 1.5 123.1 1.000 3442.7
22 22 15.0 +85.7420 (+085 44 31.0) -53.6839 (-53 41 02.2) 100.1
518.4 2.5 122.0 0.999 3408.7
22 22 30.0 +86.5987 (+086 35 55.3) -54.1756 (-54 10 32.1) 101.2
523.5 3.2 121.2 0.998 3392.4
22 22 45.0 +87.2723 (+087 16 20.2) -54.5898 (-54 35 23.2) 102.1
527.2 3.8 120.6 0.998 3383.6
22 23 00.0 +87.8377 (+087 50 15.8) -54.9584 (-54 57 30.2) 102.8
530.2 4.3 120.1 0.997 3379.2
22 23 15.0 +88.3295 (+088 19 46.1) -55.2960
(-55 17 45.6) 103.5 532.6 4.7 119.6 0.997 3377.7
22 23 30.0 +88.7667 (+088 46 00.1) -55.6108 (-55 36 39.0) 104.1
534.5 5.1 119.2 0.996 3378.5
22 23 45.0 +89.1615 (+089 09 41.2) -55.9080 (-55 54 28.7) 104.7
536.2 5.5 118.8 0.995 3381.0
22 24 00.0 +89.5218 (+089 31 18.5) -56.1908 (-56 11 27.0) 105.2
537.6 5.9 118.5 0.995 3384.8
22 24 15.0 +89.8536 (+089 51 12.8) -56.4619 (-56 27 42.9) 105.7
538.7 6.2 118.1 0.994 3389.8
22 24 30.0 +90.1610 (+090 09 39.5) -56.7230 (-56 43 22.9) 106.2
539.7 6.5 117.8 0.994 3395.7
22 24 45.0 +90.4473 (+090 26 50.3) -56.9756 (-56 58 32.0) 106.7
540.5 6.8 117.5 0.993 3402.5
22 25 00.0 +90.7152 (+090 42 54.7) -57.2206 (-57 13 14.3) 107.1
541.1 7.0 117.2 0.993 3409.9
22 25 15.0 +90.9667 (+090 57 60.0) -57.4591 (-57 27 32.8) 107.5
541.6 7.3 116.9 0.992 3418.0
22 25 30.0 +91.2034 (+091 12 12.2) -57.6917 (-57 41 30.3) 107.9
542.0 7.5 116.6 0.991 3426.7
Technical Notes:
1. Times are U.T. assuming a predictive delta-T correction of 68.0s
2. A (+0.50", -0.25") correction was applied to the moon's position
to compensate for the displacement of the mean center of figure from the
dynamical center of mass.
3. DUR s = Duration in seconds using k=0.2725067 (as per
the International Astronomical Union) with no lunar limb corrections.
4. W km = Width of the path of totality in kilometers
5. ALTd = Altitude of the Sun above the astronomical horizon
in degrees
6. AZIMd = Azimuth of the Sun in degrees
7. ECCN = Eccentricity of the shadow ellipse on the hundemental
plain.
8. PERTH = distance from PERTH airport to the centerline point
in kilometers
9. For more information on these computations CLICK
HERE.
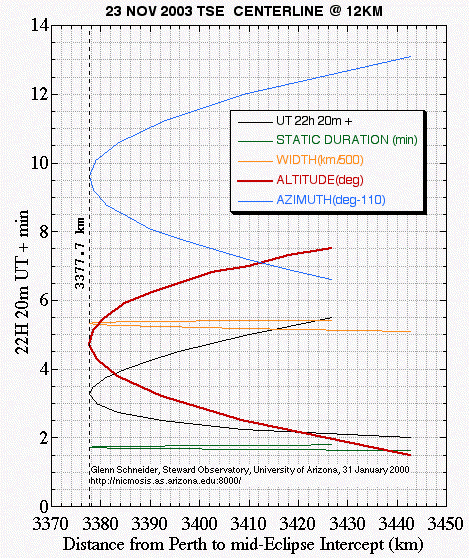
The local circumstances for a flight intercept with centerline, with the corresponding minimum flight distance is highlighted in red in the above table. Thus, the minimum total flight distance from/to Perth, Australia to observe the eclipse (plus an additional minute [or maybe a few] of flying time to encompass third contact [of course]) is approximately 4300 statute (3740 nautical) miles.
For convienience, I also show the circumstances, graphically, as a function of distance from Perth (a rather specific chart), below. Note that I have applied some offset or scaling constants to some of the centerline parameters (see legend in the Figure) to make these all convenient to see all at once at a reasonable scale. The functions are all double valued, of course, and reach minima at 3377km from Perth. If an airborne observation is planned for this mid-eclipse intercept, the Sun will stand 4.7 degrees above the astronomical horizon at mid-eclipse. While this may seem like a low solar elevation, remember at 12km (40,000 feet) the ambient in situ atmospheric pressure (using a STP profile) will only about 210 mbars, so 80% of the Earth's atmosphere will be below the aircraft yeileding a very transparent and (during totality) dark sky. The durations of totality on the the table above, and graph below, have not been adjusted to compensate for the aircraft's motion through the umbral shadow. However, to put the Sun abeam of the aircraft (i.e., "straight out the window"), the aircraft would fly perpendicular to the solar azimuth, which is largely transverse to the velocity vector of the shadow. Because of this and the intrinsically high shadow velocity at polar eclipse and near sunrise, unlike for some other eclipse geometries, the aircraft speed does not significantly affect the duration of totality. However, one can fly with the sun somewhat off-normal to the plane of the windows, to create a larger aircraft velocity component in the direction of the motion of the shadow and obtain some marginal gains in the duration of totality. This is a trade between optimum viewing angle vs. a marginal increase in totality - but a decision on that trade need not be made at this time and does not affect the issues immediately at hand. Note that the Cryodon flight, if they do target the region near Myrny, will have a static duration of totality of almost exactly two minutes (which is just 17 seconds longer than the "minimum distance" flight).

A Specific (Primary) Flight Scenario - Minimum Distance from Perth
Here a specific flight scenario is presented predicated on a mid-eclipse intercept of 22h 23m 15s, to minimize the flight distance from Perth (to reach the closest point on centerline). In following this discussion please consult this FLIGHT SCENARIO CHART. Times given assume precision navigation. Errors in position will result in errors in times and vice versa.
Note: The flight scenario described here was developed
using EFLIGHT,
a S/W package for airborne eclipse planning and navagation
1. Launch flight from Perth, Australia Airport (Latitude 31° 56'S, Longitude 115° 58'E)
2. Fly a great circle heading of 212° 21' to Latitude 54° 23' 37.9"S, Longitude 89° 14' 34.9"E. This is a distance of 3269 km (1765 nM). This point should be reached at 22:15:15 UT, so we will be 8 minutes from a mid-eclipse intercept with the center of the moon's shadow after completing a heading alignment maneuver (3). Eight minutes is somewhat arbitrary, but will provide those with photographc equipment sufficient time to re-align on the Sun after the heading of the aircraft is changed before second contact (the start of totality). The estimated flying time to this point is 4h 00m. This is assuming a cruising ground speed of 470 nM/hr plus 15 minutes accelerating to reach altitude, etc. (this additional time must be assessed by flight operations personnel). It is CRITICAL that we reach this point at that time. We CANNOT be late. Obviously, we cannot fall prey to winds aloft delaying us. Hence, an early take-off is warranted to reach allow reaching this point sufficiently ahead of time if windage estimates are not correct. If we arrive early we simply execute a circle to "hold" at that point until executing a heading alignment maneuver to put us on the centerline run. Alternatively, as we get close to that point we can adjust the airspeed to reach this point at this time. New waypoints and times can be computed in flight as needed.
3. At 22:15:15 UT while at Latitude 54° 23' 37.9"S, Longitude 89° 14' 34.9"E. execute a heading alignment maneuver to a new heading of 209.6°. This should intercept result in an intercept with the center of the moon's shadow after flying 116km (62.64 nM) at 22:23:15 U.T.
4. By holding this course at a ground speed of 470 nM/hr the edge moon's umbral shadow will overtake the aircraft at 22:22:10 U.T. at a position of Latitude 55° 11' 00.3"S, Longitude 88° 28' 59.3"S. This is sixty five seconds before maximum eclipse, noted as CII on the FLIGHT SCENARIO CHART. The instantaneous projection of the moon's shadow onto a 40,000 ft elevated Earth sphereoid is shown centered on our 22:23:15 UT intercept (green truncated ellipsoid) and also for 22:30 UT on the flight scenario chart. It is quite apparent how the projection of the moon's shadow changes very rapidly, and non-linearly in this near sun-rise portion of the path.
5. At 22:23:15 UT the aircraft will be centrally located in the moon's shadow at Latitude 55° 18' 22.4"S, Longitude 88° 21' 39.4"E. Note this is a very slightly different position then tabulated above in the 15 second granularity chart, because here I have applied a correction for atmospheric refraction with the Sun 4.8 degrees above the horizon .Holding this heading for another 4 minutes...
6. At 22:24:20 U.T. the trailing edge of the moons shadow will traverse the aircraft and bring the total phase of the eclipse to an end 65 seconds after (5) at Latitude 55° 25' 44.5"S, Longitude 88° 14' 19.4"E.
7. After another 3m 09s, at a position of Latitude 55° 44' 53.3S, Longitude 88° 18' 37.8'E (or at pilot's discretion, as the eclipse will be over!), and after traveling a total of 174km (94 nM) since entering the centerline run (3) execute another heading alignment maneuver to a new heading of 56° 26' to return to Perth. The estimated flying distance from this point to Perth is 3410km (1842 nM)
Hence, for a nominal. minimum-distance eclipse intercept
as defined above our total flight distance is approximately 3780 nM
for nominal flight conditions, and hence about an eight hour flight.
Clearly some additional margins must be budgeted.
An Alternative Flight Scenario - Minimum Distance From Melbourne
As an alternative using Melbourne as a launch point for the flight is considered, as a suitable aircraft might be easier found there than in Perth. From the Melbourne airport (Latitude 37 ° 40 'S, Longitude 144 ° 50 ' E) the closest point to the 40,000 ft. centerline of the eclipse (to the nearest kilometer in distance [and 15 seconds in U.T. along the track] is:
ECLIPSE-23NOV2003_240.DATA Topographic Elevation = 12000 meters
above MSL
HH MM SS.f LONGITUDE_______________ LATITUDE_____________ DUR
s W km ALTd AZIMd MELB km
22 30 15.0 +94.0029 (+094 00 10.6) -61.4695 (-61 28 10.3) 113.5
537.5 11.0 112.8 4360.2
We can follow a similar development as for the primary
scenario in detail. For brevity, though, the closet point to centerline
from Melbourne is 4360 km (2322 nM), thus requiring a round-trip range
appx. 1000 nM greater than the Perth to its closest point. Hence
launching from Melbourne would require an aircraft of greater capable range,
and would add appx. two hours of flying time (i.e. 10+ hours rather than
8+ hours). Indeed, to reach the same point on the centerline track
from Perth requires flying 3682.5km (1988nM). So, initiating the
flight from Melbourne to reach the centerline point closest to that airport
would require an "extra" 730nM of total travel distance (appx. 1h 33m of
flying time) compared to reaching the same point from Perth. These
seems, then, no immediate advantage of initiating the flight from Melbourne
(unless a suitable aircraft can be found there, but not in Perth).
To intercept this point potentially adds an additional constraint as it
is at 61° 28'S. I believe that commercial charter companies may
require an aircraft with more than two engines to fly beyond 60°S latitude.
This may not be the case, and needs to be verified. In and of itself
this is not an impediment, but it would rule out many potential aircraft
(if they otherwise may have the suitable range) which might be found to
launch the flight from Melbourne.
B & C) WHAT KIND OF AIRCRAFT DO WE NEED?
Clearly, the primary requisite is for any aircraft to
have an operational payload range to
meet the minimum 3780 nautical mile round-trip flight, with suitable
margins. And, it is desired that such an aircraft be the most cost-efficient
available, recognizing it would have a passenger pro-rated cost on a per-window
basis. Fuel efficiency, crew time, etc., all enter in, and only an
air charter company can address those variables. However, it is clear
that a 747 is not needed (or desired) for a dedicated eclipse flight.
Indeed, with suitable flight range a "narrow body" aircraft would be preferable
(all else being equal) as the window:seat ratio - and hence, cost per observer
is lower. This is feasible with some aircraft when one notes that
such an eclipse flight will have a VERY light payload (amd allowing a full
fuel load) . I.e., on a "narrow body" aircraft, only about 1/5 of
the capacity passenger load will be used. And, while some observers will
bring photographic equipment onboard, most will be of very modest weight
(comparable to "carry on"), and no luggage or cargo will be carried.
 As
noted before, the number of observers (and hence payload weight) will depend
upon the number of usable sun-side windows on the aircraft. Specifically,
but only for an example, it looks like the smaller of the Boeing's "next
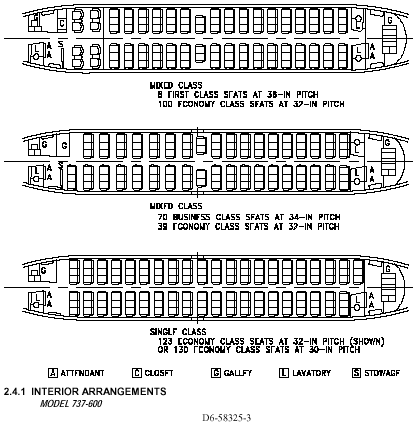
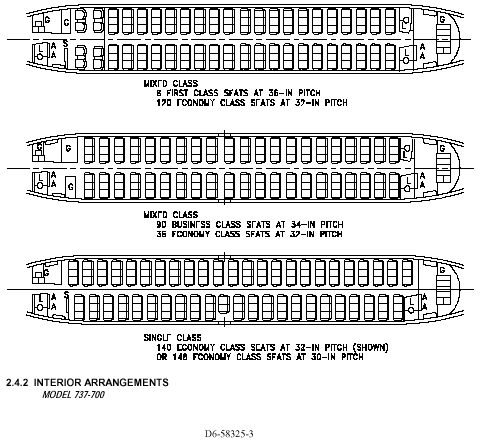
generation" 737's, the 737-600 or 737-700 could fit the bill. The
737-600 has thirty-one windows on each side, and the 737-700 has 34 (not
counting two very small windows in exit doors). The viability
of these aircraft certainly needs to be independently evaluated by someone
with specific expertise, and I do not know about the availability of a
737/600-700 in Perth. But, I discuss it here primarily in concept,
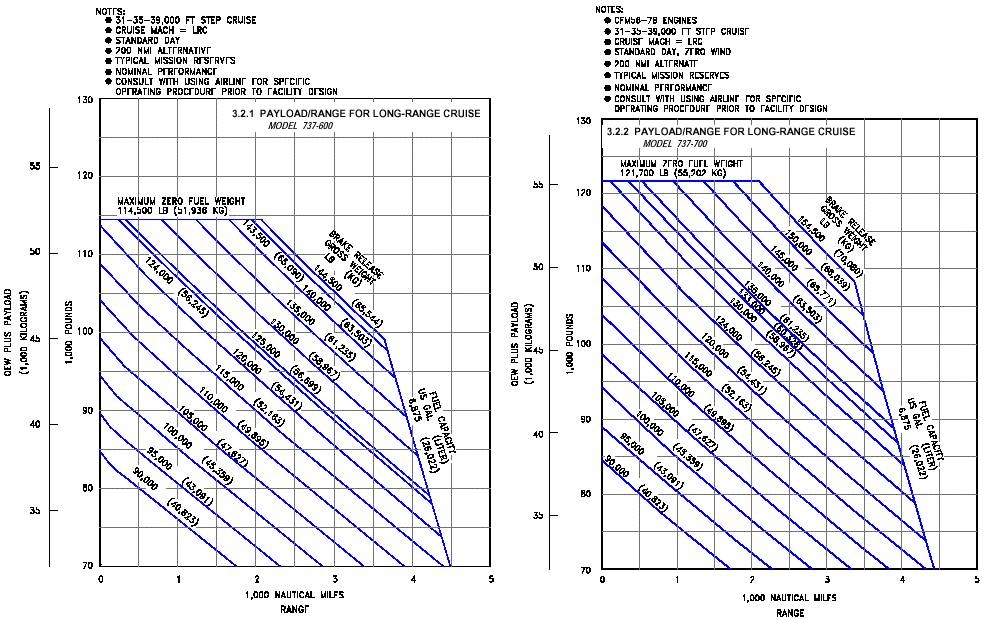
rather than specifics. The operating ranges of the Boeing 737 600/700 aircraft,
for a given "operating empty plus payload weight" may be ascertained from
appended charts by noting where the outer constraint envelope crosses the
maximum range. The Operating Empty Weight (OEW) for these aircraft are
80,200lbs and 83,000lbs, respectively. It is typically stated that
the range of a 737-600, for example, is 3230 nautical miles. But,
this is for a very height gross weight, which would not be the case.
An eclipse flight as discussed here would have a very light payload weight
(as it would have about 1/5 to 1/6 the "usual" number
of passengers).
As
noted before, the number of observers (and hence payload weight) will depend
upon the number of usable sun-side windows on the aircraft. Specifically,
but only for an example, it looks like the smaller of the Boeing's "next
generation" 737's, the 737-600 or 737-700 could fit the bill. The
737-600 has thirty-one windows on each side, and the 737-700 has 34 (not
counting two very small windows in exit doors). The viability
of these aircraft certainly needs to be independently evaluated by someone
with specific expertise, and I do not know about the availability of a
737/600-700 in Perth. But, I discuss it here primarily in concept,
rather than specifics. The operating ranges of the Boeing 737 600/700 aircraft,
for a given "operating empty plus payload weight" may be ascertained from
appended charts by noting where the outer constraint envelope crosses the
maximum range. The Operating Empty Weight (OEW) for these aircraft are
80,200lbs and 83,000lbs, respectively. It is typically stated that
the range of a 737-600, for example, is 3230 nautical miles. But,
this is for a very height gross weight, which would not be the case.
An eclipse flight as discussed here would have a very light payload weight
(as it would have about 1/5 to 1/6 the "usual" number
of passengers).
If we assume 200lbs per passenger (person plus carry-ons for eclipse, on average), and a crew of 5 (estimate) that's only 7200 and 7800 lbs., respectively, assuming all windows are filled (and without window sharing), for OEW plus payload weights of 87,400 and 90,800 lbs. As you can see from the charts, beyond the pre-allocated "typical mission reserves" this has about a 300 nautical mile further reserve for the 737-600, but a slimmer couple of hundred nautical mile reserve on the 737-700. Maybe this is cutting it too slim for this PARTICULAR aircraft, but. For a smaller number of persons, a Gulfstream IV (which typically is configured with 6 windows) might be suitable, but this too might leave little marginal range - though a Gulfstream V or V-SP (which typically has 7 windows) has more than sufficient margin. Better, something like a Falcon 900 EX would be in the same, sufficient, range class and would be preferable as it has 12 windows (and three engines). Clearly the suggestion for a particular aircraft type to meet the goals of this flight depends upon availability and such a suggestion should be left up to the knowledgeable discretion of a charter company and its pilots. Yet, the point is, if not, for example the 737-600, than another with a bit more range would do. But, I believe the basic proposition is on good footing.
Assuming these numbers (for the time being) for general
guidance, the question then is: what would be the cost for chartering an
aircraft of this type, or similar, that can meet this objective?
The nominal cruise speeds of these and similar aircrafts are about Mach
0.8, so we are talking about something close to a seven hour flight.
On a per-observer (window) basis the cost for such a charter then gets
divided by 31 or 34 (or the actual number of windows if a different aircraft).
The same question needs to be explored for a variety of aircraft, based
upon actual availabities, over the full range of number of windows.
D) WHAT NEXT?
I am seriously interested in perusing this option, and I am aware of a significant number of other people who would follow suit and opt in. I would welcome estimates and inquiries from aircraft charter companies who feel they could met these requirements, and I would be very happy to discuss this proposition with any in much more detail than covered here in this brief summary.
Personally, I have been an integral part of planning three, and executing two, very challenging high-altitude airborne eclipse observations:
1986 N. Atlantic @ 44,000 ft (Cessna Citation II from Rejkavik)
1992 S. Atlantic @ 41,000 ft (DC-10 from Rio de Janario)
2001 S. Atlantic with the AF Concorde @ 60,000 ft (from Ascension Island)
Unfortunately, the later did not occur due to the devastating
and tragic accident that grounded the Concorde fleet during the June 2001
total solar eclipse.
Please do contact me: Glenn
Schneider at: gschneider@mac.com
B737 600 and 700 Payload Range Performance Charts
B737 600 and 700 Possible Seating
Configurations are as follows: